 breakとcontinue
breakとcontinue
このステップでは、関数の「戻り値」について学習します。「戻り値」は引数の逆の動きをする存在であり、関数で処理した結果をJavaScriptに返すことが可能となります。
13.1 戻り値とは…?
まずは、「戻り値」の概要から解説していきましょう。ステップ07でも学習したように、関数を呼び出す際は、引数により関数へ値を引き渡すことが可能です。「戻り値」はこれと逆の動きをするもので、関数で処理した結果(値)を”関数の呼び出し元”へ返す機能となります。
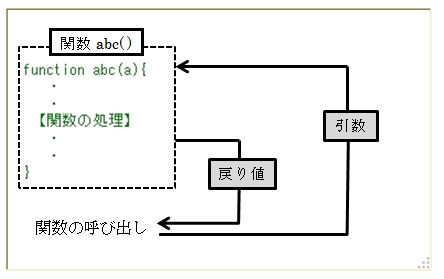
13.2 関数から戻り値を受け取るには…?
これまでは、onClickなどのイベントハンドラを使って関数を呼び出してきました。たとえば、「abc( )」という関数を呼び出す場合は「onClick="abc( )"」のように記述しました。しかし、この方法では「戻り値」を返す場所がありません。というのも、関数「abc( )」が「戻り値」を返したとしても、それを受け取る変数がないからです。これでは「戻り値」を利用することができません。
では、どのように記述すれば「戻り値」を利用できるのでしょう?その答えとなるのが、JavaScriptから関数を呼び出す方法です。JavaScriptでは、呼び出したい関数名を記述するだけで関数を実行できます。たとえば、関数「abc( )」を呼び出す場合は以下のようにJavaScriptを記述します。
もちろん、この際に数値や文字を引数として指定することも可能です。
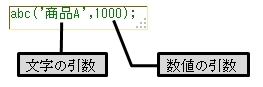
ただし、これでも「戻り値」を返す場所がないことに変わりはありません。関数から「戻り値」を返してもらい、それを呼び出し元のJavaScriptで利用するには、以下のような形式で関数を呼び出します。
変数名 = 関数名(引数1,引数2,…);
このように記述して関数を呼び出すと、関数からの「戻り値」が「=」の左辺にある変数に代入されます。もちろん、「戻り値」が代入された変数は、通常の変数と同様に扱うことが可能です。
13.3 関数から戻り値を受け取るには…?
「戻り値」を利用する場合は、「戻り値」として返す値を関数内で指定しておく必要があります。これを実行する命令がreturnです。たとえば、以下のようにreturnを記述すると、変数「x」の値を「戻り値」として返すことができます。
税込価格を計算する関数「zei( )」を例にこれまでの話をまとめると、「関数の呼び出し」~「戻り値の利用」の流れは以下のようになります。
▼Sample13_1.html
 ワンポイント
ワンポイント
関数内でreturnが実行されると、その関数の処理が強制終了されることに注意しなければいけません。このため、returnは関数に記述するのが基本となります。もし、途中にreturnを記述する場合は、if文で条件分岐を行い、その中にreturnを記述するなどの工夫が必要となります。
 ワンポイント
ワンポイント
ステップ02で解説したように、イベントハンドラの値にはJavaScriptも記述できます。むしろ、「関数名( )」で関数を呼び出す場合も、イベントハンドラの値に“関数を呼び出すJavaScript”を記述していると考えられるでしょう。これを応用すると、以下のようにイベントハンドラで関数「戻り値」を扱うことも可能となります。

13.4 戻り値を利用したJavaScriptの例
最後に「戻り値」を有効に活用した例を紹介しておきましょう。次は、2つの数値の最大公約数を求めるJavaScriptで、最大公約数を探し出す部分を関数で処理しています。このように何回も実行する処理を関数化しておくと、引数を指定して関数を呼び出すだけで何パターンもの計算結果を表示できます。
▼Sample13_2.html
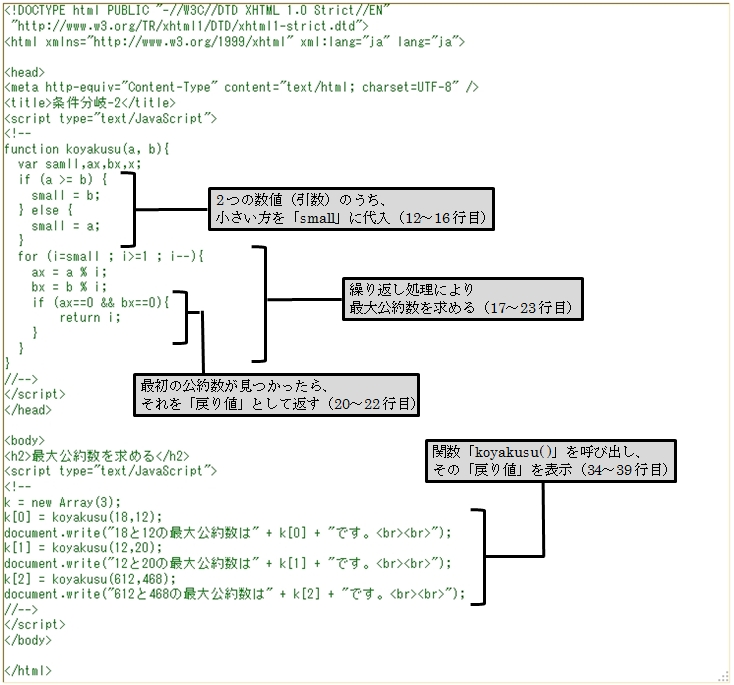
最大公約数を求める
このJavaScriptの主なポイントは以下のとおりです。
≪関数を呼び出すJavaScriptのポイント≫
・33行目
配列「k」を宣言しています。この配列には、関数「koyakusu( )」により求められる最大公約数が代入されます。
・34、36、38行目
最大公約数を求める2つの数値を引数とし、関数「koyakusu( )」を呼び出します。また、その「戻り値」を配列「k」に代入します。
・35、37、39行目
求められた最大公約数(配列「k」)をホームページ内に表示します。
≪関数「koyakusu( )」のポイント≫
・12~16行目
引数として渡された2つの数値(変数「a」と変数「b」)を比較し、値が小さい方を変数「small」に代入します。
・17~23行目
繰り返し処理により最大公約数を求めます。最大公約数が「small」を超えることはないため、繰り返しの変数「i」「small」~1まで値を1ずつ減らしながら変化させます。
・18、19行目
変数「a」「b」を「i」で割った場合の余りを変数「ax」「bx」に代入します。なお、「i」が公約数であった場合、変数「a」「b」はともに「i」で割り切れるため、「ax」「bx」の値は両方とも0になります。
・20~22行目
「ax」「bx」が両方とも0になった場合、そのときの「i」を「戻り値」として返します。同時に、関数「koyakusu( )」も強制終了されます。なお、変数「i」は大→小と変化していくため、最初に「真」となった変数「i」が最大公約数になります。
演習
(1)「Sample13_2.html」を参考に、18と12、12と20、612と468の最小公倍数を求めるホームページを作成してみましょう。
最小公倍数
※最小公倍数は関数「kobaisu( )」で求めます。
※関数「kobaisu( )」の処理手順
①引数として渡された「a」「b」を比較し、大きい方を変数「large」に代入します。
②「a」×「b」の値を変数「max」に代入します。
③「large」から「max」まで1ずつ増加する変数「i」により繰り返し処理を行います。
④繰り返し処理では、「i」が「a」と「b」の両方で割り切れるかを判定します。そして、ともに割り切れる場合の「i」を「戻り値」として返し、関数「kobaisu( )」を強制終了させます。
※ここに直接入力できます。↓↓(テキストボックスのサイズは、右下の角をドラッグすると調節できます。)
→STEP12へ
→STEP14へ